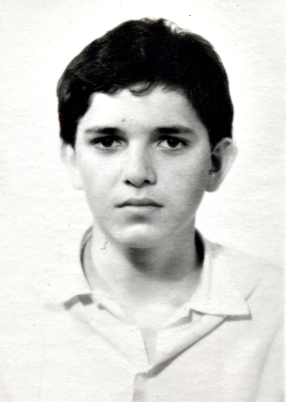 This story happened in the summer of 1975. I was 16. Before that, I was naive and brainwashed; by the end of the summer I had grown up. All that summer I was stunned and didn’t know what to do as I watched this story unfold.
This story happened in the summer of 1975. I was 16. Before that, I was naive and brainwashed; by the end of the summer I had grown up. All that summer I was stunned and didn’t know what to do as I watched this story unfold.
I was invited to the summer training camp for the International Math Olympiad. There I became friends with a fellow team member Sasha (Alexander) Reznikov. Sasha had dreamed of being a mathematician from childhood. He was gifted and brilliant and when he was in the 7th grade he got noticed by professional mathematicians. They told him that the only way to become a mathematician is to do undergraduate studies at the math department of Moscow State University. He was also told that the math department doesn’t accept Jews. Sasha was Jewish.
But there was a hole in the system. If he could get to the International Math Olympiad, he would be admitted to the place of his choice by an order of the Ministry of Education. As the IMO was conducted during entrance exams for universities, there was this special arrangement for the team members. Besides, the Soviet Math Olympiad wasn’t yet corrupted, so the Olympiads would give him a chance.
Sasha was brilliant, but he had a disadvantage — he was 2 years younger than his classmates because he had skipped grades. Since the IMO is only for high school students, he had to make it to the IMO before he graduated at 15 years old.
He worked very hard and really pushed himself, and he made it on to our team. The photo of two kids is of Sasha and me that summer.
We had a supervisor — Zoya Ivanovna — who was a Ministry liaison. She was to compile the list of team members for the Ministry of those who should be accepted without entrance exams to universities and colleges. The team had eight people, so every year the list consisted of eight students. That year was special, since we actually only had six people on our team who were high school seniors. Two of us, Sergey Finashin and I, were not yet seniors. But Zoya Ivanovna who was a good-hearted lady decided to sneak in eight people and added our two alternates to the list. As our alternates were preparing for the IMO instead of preparing for entrance exams, this was a generous and fair thing to do. Everything was fine and everyone was happy.

Until one day when strange things started to happen. We were invited for a meeting where Zoya Ivanovna told us that there was a problem with Moscow State University. We were told that the math department has a limit of four people who can be accepted without an entrance exam, and we had five students applying. Zoya Ivanovna asked if there was a volunteer who might reconsider. At this point Alexey Muzykantov said that he would volunteer since he was an alternate. Besides, he was always as interested in physics as in math, and would be happy to study in the physics department.
After the meeting I stumbled upon Zoya Ivanovna crying in the ladies room. She told me that she didn’t know what to do. The problem was that out of five people applying for the math department of Moscow State University, three were Jews. Three Jews were too many out of the 400 people annually accepted to the department. Our team coordinator, Valentin Anatolievich Skvortsov, was working at the math department, where he was being pressured. Zoya Ivanovna told me he had been threatened with expulsion from the Communist Party if he didn’t reduce the number of Jews by at least one. Being expelled from the Communist Party was a serious threat at that time and Zoya Ivanovna was eager to help, so she invented this idea about the limit. The idea didn’t work, because Alexey Muzykantov, who removed himself from the list, wasn’t Jewish.
After several days, Sasha Reznikov’s mother appeared at the summer program. She told me that she was being pushed to persuade Sasha not to go to Moscow State University.
I asked Zoya Ivanovna why she chose Sasha. She told me that out of the three Jews, one was from Moscow, so she didn’t consider him, and Sasha was much younger than the third student and, besides, he had health problems. So she tried to convince Sasha’s mother that Sasha would be better off in his home town Kiev than in Moscow.
Sasha went to Kiev University. The system had had a hole through which two Jews passed that year, so even though Sasha had made astonishing efforts, he hit a wall. He was crushed.
Later he tried to transfer to Moscow State University, but was ridiculed, humiliated and denied. Eventually Sasha moved to Israel and got his PhD in mathematics. He died in 2003 by, according to rumors, suicide.
Share:





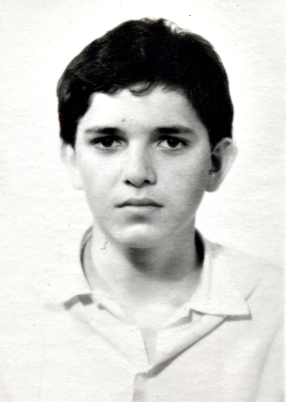 This story happened in the summer of 1975. I was 16. Before that, I was naive and brainwashed; by the end of the summer I had grown up. All that summer I was stunned and didn’t know what to do as I watched this story unfold.
This story happened in the summer of 1975. I was 16. Before that, I was naive and brainwashed; by the end of the summer I had grown up. All that summer I was stunned and didn’t know what to do as I watched this story unfold.
 I bought the book “
I bought the book “ I am celebrating the first hundred essays I have written for my blog. My English teacher and editor Sue Katz edited most of them. Sue Katz not only corrects my English mistakes, but also helps me to choose better and more descriptive words and rearranges my text so that it doesn’t sound like a direct translation from Russian.
I am celebrating the first hundred essays I have written for my blog. My English teacher and editor Sue Katz edited most of them. Sue Katz not only corrects my English mistakes, but also helps me to choose better and more descriptive words and rearranges my text so that it doesn’t sound like a direct translation from Russian.