Points on the Plane
This geometric problem was given to me by Arkady Berenstein:
There are n points on the plane, but not all of them are on one line. Prove that a line exists that passes through exactly two points of this set.
Arkady gave me a beautiful solution to this problem. First, draw a line through each pair of points. Suppose you calculate all the distances from each point to all the lines that the point doesn’t belong to. Pick the smallest distance. The corresponding line will be the one with two points. To finish the solution you need to fill in the details. That process is usually left to the reader.
I suspect that there might also be a solution using linear algebra. Can you find one?
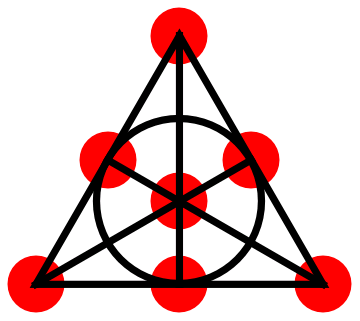I would like to reformulate this problem without using geometry. Suppose there is a set of n elements. Let’s call a family of subsets line-like if any two distinct subsets of this family can have as an intersection not more than one element. Then the geometry problem above has a set-theoretical analogue:
You have a set of n elements and a line-like family of subsets of this set such that any two elements of the set belong to a subset from this family, and that the family doesn’t contain the whole set. Is it true that there always exists a subset in this family consisting of two elements?
Usually I give such problems as homework for the reader, but this time I decided to change my habit, so I’m including the picture which contains the solution of this problem by my son Alexey Radul.
Conclusion: geometry is important.
Gerhard:
The geometric statement is the so-called Sylvester–Gallai theorem:
https://en.wikipedia.org/wiki/Sylvester–Gallai_theorem
The beautiful proof was found by Tibor Gallai in the 1930s.
21 September 2009, 2:48 ammisha:
Behold: the Fano plane has made its appearance again. The problem belongs to the projective geometry, while the solution given to Tanya by Berenstein uses metric. You can see a proof of the projectively dual problem that doesn’t use metric, but uses topology (the Euler characteristic) instead in a section of the page that Gerhard has already pointed out.
21 September 2009, 4:30 pmmisha:
I guess, especially as a parlor game, to those who enjoy playing it.
21 September 2009, 7:03 pmmisha:
Here is another solution that uses convexity. Take a convex hull of all these points and look at it. I don’t include any references since I am too lazy to look for them and I have never heard of this solution before.
22 September 2009, 7:33 ammisha:
I guess I have to add some details to my previous comment to make it into a solution. The convex hull of our points is a convex polygon. Let A, B and C be the consecutive vertices of this polygon. If AB or BC contain only 2 points from our set, we are done. If both of them contain at least 3 points of our set, pick D on AB and E on BC the closest to B. Cut the triangle DBE off our polygon. Now we can argue by induction on the number of points in our set.
22 September 2009, 10:25 pmmisha:
It looks like induction doesn’t work, since we threw away the point B. Oh, well, the solution is wrong, maybe someone can figure out how to fix it.
23 September 2009, 3:23 amDavid Wilson:
The Sylvester-Gillai theorem (for any finite noncollinear set of points S, a line exists passing through exactly two points of S) holds for the real projective plane (the extension of the Euclidean plane to a projective plane) but not for the Fano projective plane your son provided as a counterexample. This means that Sylvester-Gillai theorem is independent of the projective plane properties (two distinct points lie on a unique line and two distinct lines intersect at a unique point).
The standard proof of the Sylvester-Gillai for the Euclidean plane that you hinted at (which fairly easily generalizes to the real projective plane), uses the fact that the Euclidean plane is metric space (has a real-valued point distance function satisfying the triangle inequality). The metric space properties are non-topological (they are the “geometry” in “geometry counts”). This standard proof can only conceivably be generalized to other metric spaces.
However, I was wondering if there might not be a topological proof of Sylvester-Gillai. Specifically, I noticed that the line separation theorem (a line divides the rest of the plane into two disjoint halfplanes, such that a segment between two points off the line crosses the line iff the points are in different halfplanes). Plane separation is a topological property, and holds for the Euclidean plane and the real projective plane, but not for the Fano plane, just like Sylvester-Gillai. I was wondering if there might not be a topological proof of Sylvester-Gillai based on plane separation.
23 September 2009, 9:21 pmnick the greek:
I have to say that by looking at the problem the first thing that crossed my mind was induction.But i couldn’t seem to find how to do it!!!Then i thought,hey, why don’t i try an indirect proof? Here is my point of view:
If there actually isn’t a line containing exactly two points in the plane,then it follows that for every line defined by two arbitrary points there has to exist a third point lying on the same line.
I want to prove that if that’s the case,then all the points have to be collinear,which would contradict the initial hypothesis that not all points are collinear!This is where i use induction
1)Prove it for the smallest number possible (here that number is 3).It is quite easy to understand that if for any two out of three points there is a third lying on the same line,thenall three points are collinear!
2)Suppose the statement is true for n points,meaning that if for any two out of n points there exists a third lying on the same line,all points are collinear.
3)Finish the proof by proving it for n+1 points.Let’s suppose we have n+1 points on the plane with the property that for every two out of n+1 points there exists a third lying on the same line.If we prove that all n+1 points are collinear,we should be done!
Indeed,since all the possible choices of two points !!(out of n points)!! are all contained in the number of all the possible choices of two points out of n+1 points,it follows that n points are certainly collinear according to our assumption.Now suppose that the remaining point isn’t lying on the same line.If we draw a line from any of the n collinear points that passes through the last point ,then that line will only contain two points,which is impossible according to what we are trying to prove!
To sum up, we have proven that if there isn’t a line containing exactly two points then all the points have to be collinear,which is contradictory to the initial assumption of the problem!Therefore,there does exist one line containing exactly two points of the plane!
First of all,i would like to apologise for trying to be very descriptive in my solution,but i have been told from my teacher that this proof is wrong.However,looking at it over and over again i can’t seem to find the mistake!Please someone tell me whether my solution is indeed mistaken (or correct hopefully) and why.Also,please excuse any possible misspellings.I would like to thank all of you in advance.I will be waiting for a response.
1 May 2010, 11:35 am