Grand Tour Puzzles

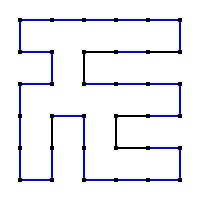
I love Grand Tour puzzles more than I love Sudoku. You are given a graph, for example, a square grid like the one on the left. Some edges are highlighted. You need to find a closed path that visits each vertex exactly once and includes the highlighted edges as part of the path. Mathematically speaking you need to reconstruct a Hamiltonian circuit on a graph, once you are given a part of it. The highlighted edges are chosen to guarantee a unique solution to the puzzle.
On the left you can see a sample grand tour problem with its solution. This puzzle was designed by Glenn Iba. On Glenn’s Grand Tour Puzzle Page you can find many grand tour puzzles of varying levels of difficulty. The puzzles are playable. That is, you can click or unclick an edge. You can also branch out in a different color, which is especially useful for difficult puzzles when you want to test a hypothesis. I just want to warn you: these puzzles are addictive — I couldn’t stop playing until I solved all of them.
Below there is a simple grand tour puzzle from Glenn’s collection, but this time on a triangular grid:
You do not need a grid to construct a puzzle. But these puzzles look very natural on grids. I tried to analyze square grid puzzles a little bit. The first important point is that for square grids with odd number of vertices on each side of the square, Hamiltonian cycles do not exist. This point is easier to prove for directed Hamiltonian cycles. You can make a directed cycle from an undirected one by choosing a direction. If you have a directed cycle on a square grid, then the number of edges pointing up should be the same as the number of edges pointing down. We can say the same thing about edges on the cycle pointing left or right. Hence, the number of edges of a Hamiltonian cycle on a square grid should be even. At the same time, the number of edges of any Hamiltonian cycle equals the number of vertices.
I just proved that you need only consider square grids with an even number of vertices on each side. For square grids with two vertices on each side, there is only one Hamiltonian cycle, namely the border of the square. The only grand tour puzzle for this grid won’t have highlighted edges at all. For a square grid with four vertices on each side there are only two different Hamiltonian cycles up to isomorpshisms:
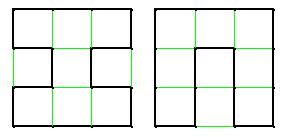
If we count all the reflections and rotations, we will get six Hamiltonian cycles. The next picture shows all 11 grand tour puzzles on this grid. If we count rotations and reflections, we will get 66 different grand tour puzzles.
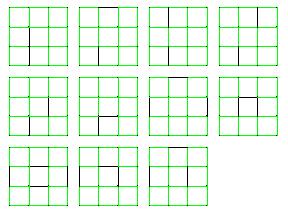
Below are the sequences associated with this puzzle. Except for one case, I do not know if these sequences are in the Online Encyclopedia for Integer Sequences. I don’t know because I only counted two terms of each sequence, and this information is not sufficient to identify the sequence.
- A003763 Number of Hamiltonian cycles on 2n by 2n square grid of points. The sequence starts 1, 6, 1072, ….
- Number of Hamiltonian cycles up to isomorphism on 2n by 2n square grid of points. The sequence starts 1, 2, ….
- Number of Grand Tour puzzles on 2n by 2n square grid of points. The sequence starts 1, 11, ….
- Number of Grand Tour puzzles up to isomorphism on 2n by 2n square grid of points. The sequence starts 1, 66, ….
- The smallest number of edges in a Grand Tour puzzle on 2n by 2n square grid of points. The sequence starts 0, 2, ….
- The largest number of edges in a Grand Tour puzzle on 2n by 2n square grid of points. The sequence starts 0, 4, ….
If you look at Glenn Iba’s 6 by 6 square grid puzzles, you can see that the smallest number of edges is not more than 6. And the largest number of edges is no less than 12.
You can also make similar sequences for a triangular grid.
I invite you to calculate these sequences and submit them to the OEIS, if they are not already there.
Share:
Grand Tour Puzzles » puzzlinks.com:
[…] puzzles on the web here. Also, for anyone interested in the math behind the puzzle, check out this page. Enjoy! Tags: grand-tour,puzzles Posted by Josh in Types/Variations (Saturday August 16, […]
16 August 2008, 5:45 am~ÔttÔ~:
With consent of Glenn Iba you can find an online version of his puzzles here:
https://www.janko.at/Raetsel/Grand-Tour/
~ÔttÔ~
12 July 2009, 1:20 amFun With Puzzles:
Thanks for introducing this puzzle type. Link to “Grand Tour Puzzle Page” on this page is not working and needs to be corrected.
2 June 2012, 6:15 amTanya Khovanova:
Grand Tour moved:
https://glenniba.com/grandtourhexbranch/GrandTour.html
3 June 2012, 6:59 pm2013-03-01 | Galvosūkykla:
[…] Sujungimo pavyzdžiai. […]
1 March 2013, 3:13 am