L-Reptiles
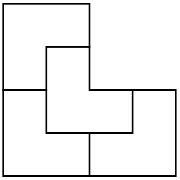 I remember a math problem from my childhood: divide an L-shaped triomino into four congruent parts. The answer is in the picture on the left. Such division is quite appropriately called a reptile (repetitive tiling). Solomon Golomb invented the name many years ago. He wasn’t aware that his definition would end up creating Googling problems, for when you search for such a mathematical object you will stumble upon a lot of amphibians.
I remember a math problem from my childhood: divide an L-shaped triomino into four congruent parts. The answer is in the picture on the left. Such division is quite appropriately called a reptile (repetitive tiling). Solomon Golomb invented the name many years ago. He wasn’t aware that his definition would end up creating Googling problems, for when you search for such a mathematical object you will stumble upon a lot of amphibians.
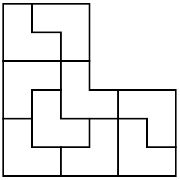
Similarly, you can divide the same shape into 9 congruent pieces (see the figure on the left).
Suppose you want to divide a shape into pieces that are similar, but not necessarily of the same size. Such tiling is called an irreptile (irregular reptile).

At the Gathering for Gardner 9 I listened to Carolyn Yackel‘s talk about the L-reptiles and L-irreptiles. One of the ways to create an irreptile is to start with a reptile, then to make a sub-tiling of one of the existing tiles. This procedure can be repeated many times.
Carolyn brought a ceramic table to the Gathering for Gardner. This table is made of two L-shapes. Both shapes are irreptiles, created by this procedure. In one part of the table she started with a 9-reptile, and in the other with a 4-reptile. She sent me this picture of her table to use in this essay.
After her talk I started wondering how many tiles can an L-irreptile be comprised of. We start with one piece: the L-shape itself. If we divide a tile into four smaller tiles we add three more pieces. If we divide it into nine tiles we add eight more pieces. We can mix sub-dividing into four and nine tiles. The total number of tiles that an L-shape can be comprised of by this procedure is all the numbers you can get from 1 by adding three or eight. The sequence is 1, 4, 7, 9, 10, 12, 13, 15, 16, 17 and so on. Starting from 15 we get all the consecutive numbers.
The numbers that are not represented in the above sequence are 2, 3, 5, 6, 8, 11 and 14. Can we divide an L-shape into such numbers of tiles? Benoît Jubin reminded me that there is an L-reptile with six pieces.
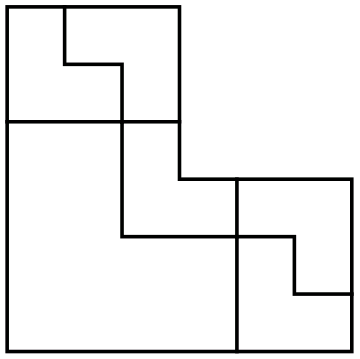
Consequently, we can add 5 more pieces to any L-irreptile. Thus, there exists an L-irreptile made out of 11 (1+5+5) and out of 14 (1+8+5) pieces. The numbers that are left are 2, 3, 5 and 8.
While I was discussing L-irreptiles with fans of sequences, David Wilson suggested a conjecture.
David Wilson’s conjecture. If there is an L-irreptile, there is a corresponding square-irreptile with similarly-sized pieces.
If this conjecture is true, then we can see that L-irreptiles with 2, 3 or 5 pieces can’t exist as corresponding square-irreptiles do not exist.
For example, to prove that 2 or 3 square-irreptiles can’t exist, you need to notice that each corner of the square we are trying to tile should belong to a different small tile.
The question of the existence of an 8-irreptile of the L-shape is more interesting and challenging. The square 8-irreptile exists. If you can prove that the L-shape 8-irreptile doesn’t exist, then you will automatically prove that the converse to Wilson’s conjecture is not true.
Share:
David Wilson:
Actually, it is not too hard to show that the square 8-irreptiles 3,1,1,1,1,1,1,1 and 3,2,2,2,1,1,1,1 have no corresponding L-irreptile, so the converse conjecture is not true.
More interestingly, does any polyomino irreptile not have a square irreptile?
16 April 2010, 10:24 pmcolorblind:
“Benoît Jubin reminded me that there is an L-reptile with six pieces.”
Maybe I’m missing something here. Suppose there is an L-reptile of area 3(long side length 2, short side 1). If there is an L-reptile with six pieces, then each piece has an area of 1/2. From that, we can deduce each piece has a long side of sqrt(2)/sqrt(3). That is irrational, therefore there is no additive combination of such pieces that would fit completely into a side of 1 or 2 as they would be irrational also.
I’ll leave as an exercise to show this is also true for an L-irreptile also. (OK, I’m lazy…but the argument should be similar – there would need to be at least one irrationally sided piece.)
17 April 2010, 10:00 amcolorblind:
….As I look at the pic of the L-irreptile…. *doh*
17 April 2010, 10:05 amJoseph DeVincentis:
We are discussing the generalization of this subject for other polyominoes at Math Magic this month. See https://www2.stetson.edu/~efriedma/mathmagic/ and also the best current results at https://www2.stetson.edu/~efriedma/mathmagic/0810.html
16 August 2010, 10:04 am