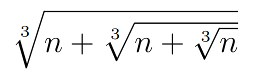Calculating the Average Age in Secret
Oskar van Deventer is a designer of beautiful mechanical puzzles. For the recent mini-MOVES gathering at the MoMath, he asked people in his Zoom breakout room to calculate the average age in the room without revealing their actual ages. I know the following solution to this puzzle.
People agree on a large number N that is guaranteed to be greater than the sum of all the ages. The first person, say Alice, thinks of a uniformly random integer R between 0 and N. Alice adds her age to R modulo N and passes the result to the second person, say Bob. Bob adds his age modulo N and passes the result to the third person, and so on. When the result comes back to Alice, she subtracts R modulo N and announces the sum total of all the ages.
During this process, no one gets any information about other people’s ages. But two people can collude to figure out the sum of the ages of the people “sitting” between them.
I gave this problem to my grandson, and he suggested the following procedure. First, people choose two trusted handlers: Alice and Bob. Then, each person splits their age into the sum of two numbers (the splitting should be random and allow one of the numbers to be negative). They then give one number to Alice and another to Bob. Alice and Bob announce the sums of the numbers they receive. After that, the sum total of everyone’s ages is the sum of the two numbers that Alice and Bob announce.
The advantage of this method is that no two people, except Alice and Bob, can collude to get more information. The disadvantage is that if Alice and Bob collude, they would know everyone’s age. Which method would you prefer?
Share:Weird Ways to Improve Your Erdős Number
Many years ago, I wrote a blog post about an amusing fact: John Conway put Moscow, the former capital of the USSR, as a coauthor: A Math Paper by Moscow, USSR. Thus, Moscow got an Erdős number 2, thanks to Conway’s Erdős number 1. At that time, my Erdős number was 4, so I wondered if I should try coauthoring a paper with Moscow, my former city of birth, to improve my Erdős number.
This weird idea didn’t materialize. Meanwhile, my Erdős number became 2 after coauthoring a paper with Richard Guy, Conway’s Subprime Fibonacci Sequences. I relaxed and forgot all about my Erdős status. I couldn’t do better anyway, or could I?
I recently heard about a cheater who applied to grad schools. In addition to a bunch of fabricated grades, the cheater submitted an arXiv link to a phony paper. What is fascinating to me is that the cheater put real professors’ names from the university the cheater supposedly attended as coauthors. The professors hadn’t heard of this student and had no clue about the paper. So the cheater added fake coauthors to add legitimacy to their application and boost the perceived value of the cheater’s “research”. As a consequence, the cheater got a fake Erdős number.
I hope that the arXiv withdrew the paper. Cheating is the wrong way to improve one’s Erdős number.
But here is another story. Robert Wayne Thomason named as coauthor his dead friend, Thomas Trobaugh. The paper in question is Higher Algebraic K-Theory of Schemes and of Derived Categories and can be found at https://www.gwern.net/docs/math/1990-thomason.pdf. This paragraph in the paper’s introduction explains the situation.
The first author [Robert Wayne Thomason] must state that his coauthor and close friend, Tom Trobaugh, quite intelligent, singularly original, and inordinately generous, killed himself consequent to endogenous depression. Ninety-four days later, in my dream, Tom’s simulacrum remarked, “The direct limit characterization of perfect complexes shows that they extend, just as one extends a coherent sheaf.” Awaking with a start, I knew this idea had to be wrong, since some perfect complexes have a non-vanishing K0 obstruction to extension. I had worked on this problem for 3 years, and saw this approach to be hopeless. But Tom’s simulacrum had been so insistent, I knew he wouldn’t let me sleep undisturbed until I had worked out the argument and could point to the gap. This work quickly led to the key results of this paper.
This precedent gives anyone hope that they might achieve an Erdős number 1. You just need to wait for Paul Erdős to come to you in your dreams with a genius idea.
Share:
Fun with Latin Squares
Last year, our junior PRIMES STEP group studied Latin squares. We invented a lot of different types of Latin squares and wrote a paper about it, Fun with Latin Squares. Recall that a Latin square is an n by n table containing numbers 1 through n in every cell, so that every number occurs once in each row and column. In this post, I want to talk about anti-chiece Latin squares.
First, what’s a chiece? A chiece is a portmanteau word made out of two words, chess and piece, and, not surprisingly, it means a chess piece. Given a chiece, an anti-chiece Latin square is a Latin square such that any two cells, where our chiece can move from one cell to the other, according to the rules of chess, can’t contain the same number. Let’s see what this means.
Let’s start with rooks, which move along rows and columns. An anti-rook Latin square can’t have the same numbers repeating in any one row or column. Ha, anti-rook Latin squares are just Latin squares. Anti-bishop and anti-queen Latin squares can’t have the same numbers repeating on any diagonal.
Now, here is a picture of an anti-knight Latin square in which no two identical numbers are a knight’s move apart. This particular Latin square also forms a mini-Sudoku: not only does each row and column, but also each 2 by 2 corner region, contains all distinct numbers.
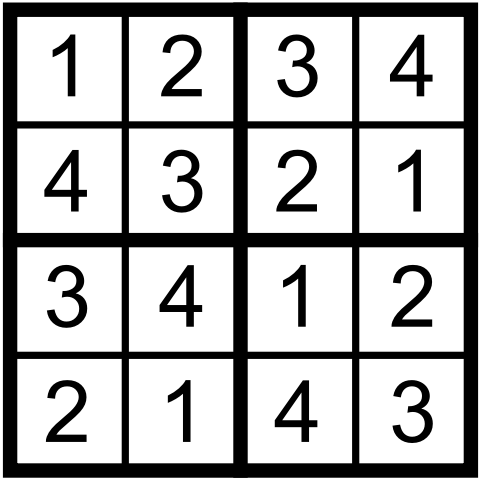
Consider all instances of some number, say 1, in an anti-chiece Latin square. If the board is n by n, we get n instances of non-attacking chieces. A famous math puzzle asks to place eight non-attacking queens on a standard chessboard. So the instances of any one particular number in an anti-queen Latin square solves the problem of placing n non-attacking queens on an n by n chessboard. Thus, building an anti-queen Latin square is more complicated than solving the non-attacking queens puzzle. The former requires filling the chessboard with n non-overlapping sets of non-attacking queens. The picture below gives an example of an anti-queen 5 by 5 Latin square.

This square has some interesting properties. It can be formed by cycling the first row. It also happens to be one of the chiece Latin squares we study in our paper. A chiece Latin square is a Latin square such that for each number in a cell, there is another cell, a chiece’s move apart, containing the same number. You can check that our anti-queen Latin square is at the same time a knight Latin square.
I wonder, can anyone build an anti-queen Latin square on the standard 8 by 8 chessboard?
Share:
The Barber Paradox and English Tenses
Here is the famous barber paradox.
Paradox. The barber shaves all those and only those who don’t shave themselves. Does the barber shave himself?
If he shaves himself, then he doesn’t shave himself. If he doesn’t shave himself, then he shaves himself.
English is not my primary language, and I am fascinated by the variety of verb tenses in English as compared to the Russian language. For example, Russian has one present tense while English has four. I wonder what would happen if we use the other present tenses in this paradox.
Present continuous. The barber shaves all those and only those who aren’t shaving themselves. Does the barber shave himself?
Does this mean that the barber starts shaving himself and then has to stop, and a moment later he has to start again?
Present perfect. The barber shaves all those and only those who haven’t shaved themselves. Does the barber shave himself?
Does this mean that the barber shaves himself every other day?
Present perfect continuous. The barber shaves all those and only those who haven’t been shaving themselves. Does the barber shave himself?
Does this mean the barber shaves himself once in his lifetime and then never again?
Share:The Age of Consent
Tim Gowers discussed the age of consent on his blog, which I can no longer find. I will talk about his post here based on my old notes and my memory. The age of consent is a legal term to protect young people from being manipulated into agreeing to sex. Having consensual sex with people under the age of consent may be considered statutory rape or child sexual abuse.
Gowers starts with several assumptions.
- Non-triviality: There should exist an age at which a person is qualified to consent to sex and, consequently, have it.
- Simplicity: Whether or not two people are allowed to have sex with each other should depend only on their age in years.
- Monotonicity: If two people are allowed to have sex with each other today, they should be allowed to have sex with each other at all times in the future.
From these assumptions, the following theorem can be deduced.
Theorem. The only possible rule satisfying these assumptions would allow any two people to have sex with each other as long as they both reached some fixed age k.
There is a problem with this type of rule. Suppose k is 18. If two people who are slightly younger than 18 have consensual sex, they can’t both be predators. These are two children with raging hormones. There is no reason to punish anyone. Now imagine that one of the partners turns 18. Society would still consider this a Romeo-and-Juliet case and would tend not to punish such a partner. Now imagine a child younger than 18 having sex with a partner over 40. The older partner has no raging hormones, knows what they are doing, and probably knows how to manipulate little children into having sex. So, it might be desirable to have a rule that differentiates between these two cases. The rule would take into account the difference in ages while forgiving younger offenders and still punishing predators.
Consider the most common type of law to resolve this issue: Anyone older than 18 can have sex, and, in addition, a person who is not older than 20 can have sex with someone between the ages of 16 and 18. This law doesn’t satisfy monotonicity. It could be that one day the older partner is not yet 20, and the next day, oops, they have a birthday. So, as a birthday gift, they are not allowed to have sex with each other anymore.
Here is a simple idea to resolve the issue by having the law focus on the age gap instead of the age of the older partner. We can have an adjusted law: Anyone older than 18 can have sex, and, in addition, a person can have sex with someone between the ages of 16 and 18 as long as the age gap is not more than four years. This rule doesn’t satisfy the simplicity assumption above, but it is simple enough. It is close in spirit to the previous rule and satisfies monotonicity. The problem with this rule is continuity.
- Continuity: If the age gap between couple A is only slightly larger than the age gap between couple B, then couple A should not have to wait significantly longer to be allowed to have sex.
According to the adjusted rule, the couple with the age gap of four years and one day might have to wait two years longer to have sex than the couple with the age gap of four years. This seems unfair.
Tim Gowers suggests dropping the simplicity rule. We can use days rather than years. For example, the rule might be that if one person in a couple is under 18, but at least 16, and has age x, then the other partner has to be not more than age y, where for example, y − x = 4 + (x − 16)/2. So when one partner turns 16, their partner has to be not older than 20. When one partner is 16 and two months, the other cannot be older than 20 and three months. With the younger partner getting older, the allowable age gap is increasing slowly. By the time the younger partner is a day from turning 18, their partner can be almost five years older.
It might be complicated for two people to calculate if they are allowed to have sex according to this formula. But Gowers’ big idea was that apps and websites could do this easily: two people plug in their birthdays and know whether they are allowed to have sex.
Share:Reversible Tetrahedra
Do you know what an isosceles tetrahedron is? I didn’t until recently. An isosceles tetrahedron has all of its faces congruent. Equivalently, all pairs of opposite edges are of equal length. Such tetrahedra are also called disphenoids. Here are some cute statements about them.
- If the four faces of a tetrahedron all have the same perimeter, then the tetrahedron is a disphenoid.
- If the four faces of a tetrahedron all have the same area, then the tetrahedron is a disphenoid.
Disphenoids have three nontrivial symmetries: 180-degree rotations around three lines connecting the midpoints of opposite edges.
Is it possible to have a tetrahedron with fewer symmetries than disphenoids? Yes, it is. Dan Klain just published a fascinating paper about such tetrahedra: Tetrahedra with Congruent Face Pairs. The results are so elegant and simple that I was surprised that they were new. I got curious and started to google aggressively. I found an official name for this kind of tetrahedron: phyllic disphenoid, but no theorems about them. Their name is quite unappealing: no wonder people didn’t want to study them much. Obviously, Dan wasn’t as aggressive at googling, so he didn’t find this official name and called them reversible tetrahedra. But my favorite name for them is the name Dan thought of but didn’t use in his paper: bi-isosceles tetrahedra.
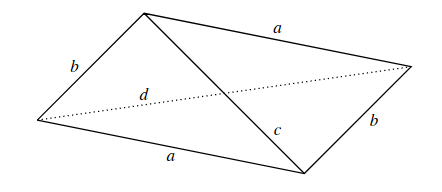
Here is the picture of a bi-isosceles tetrahedron from Dan’s paper. It has two faces with sides a, b, and c, and two faces with sides a, b, and d. The edges of this tetrahedron are: a, a, b, b, c, and d. It has one nontrivial symmetry: a 180-degree rotation around the line connecting the midpoints of the unequal opposite edges c and d. The picture emphasizes this symmetry. The figure in the picture is a projection of a bi-isosceles tetrahedron onto a plane, such that the line of symmetry is projected onto the point of symmetry of the projection. The two cute statements above, about disphenoids, can be generalized to the case of bi-isosceles tetrahedra.
- If the four faces of a tetrahedron can be split into two pairs with the same perimeter, then the tetrahedron is bi-isosceles.
- If the four faces of a tetrahedron can be split into two pairs with the same area, then the tetrahedron is bi-isosceles.
The first property is trivial, while the second one is proven in Dan’s paper. Dan also shows how to calculate the volume of a bi-isosceles tetrahedron:
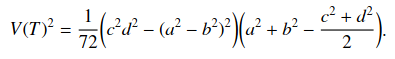
Share:
The Problem with Two Girls
Puzzle. Two girls were born to the same mother, at the same time, on the same day, in the same month, in the same year, and yet somehow they’re not twins. Why not?
I won’t tell you the expected answer, but my students are inventive. They suggested all sorts of scenarios.
Scenario 1. There are two different fathers. I had to google this and discovered that, indeed, it is possible. This phenomenon is called heteropaternal superfecundation. It happens when two of a woman’s eggs are fertilized by sperm from two different men. Unfortunately for my students, such babies would still be called twins.
Scenario 2. The girls are born on the same date, but not on the same day. This could happen when transitioning from the Julian to Gregorian calendar. The difference in birth times could be up to two weeks. I had to google this and discovered that twins can be born months apart. The record holders have a condition called uterus didelphys, which means that the mother has two wombs. Unfortunately for my students, such babies would still be called twins.
Scenario 3. The second girl is a clone. This scenario can potentially happen in the future. Fortunately for that student, I suspect that such babies would be called clones, not twins.
I decided to invent my own scenario outside of the actual answer, and I did.
Scenario 4. Two girls are from the same surrogate mother, but they are not twins. I had to google this and discovered that this actually happened: Surrogate mother of ‘twins’ finds one is hers.
Sometimes life is more interesting than math puzzles.
Share:Martin Gardner’s Surprise

In his article on Möbius strips, Martin Gardner included a cute construction.
Construction. Cut out a cross from a piece of paper. Then glue one pair of opposite ends to make a cylinder and the other pair to make a Möbius strip. Then Martin instructs, “Trisect the twisted band, then bisect the untwisted one, and open up for a big surprise!”
In my effort to reuse Möbius strips, I started making them out of zippers. So Martin’s construction had its destiny zipped. The first picture shows the construction before it is being dissected. I was quite happy with my plan to use zippers as it had its advantages over paper. For the surprise to work, the twisted band shouldn’t be cut completely. Meaning, the middle part of the Möbius strip shouldn’t be cut. I sewed my zipper monstrosity not to cause any ambiguities: there is nothing to cut, just unzip the zippers.
Little did I know that unzipping is not the issue, but zipping back up is. I tried to zip the surprise back up several times; all of them unsuccessfully, as you can see on the two other pictures. I finally had to invite the real expert — my grandson — to do it.


Share: