Archive for the ‘Puzzles’ Category.
1st October 2025, 05:51 pm
I start my homework with warm-up puzzles.
Puzzle. Two friends went for a walk and found $20. How much money would they have found if there were four of them?
The answer, of course, is $20. The number of people doesn’t change the amount of money lying around. Even ChatGPT gave this answer. Duh!
My hope was to catch them not paying attention and mindlessly multiply to get $40.
To my surprise, some of them answered $80. The ‘them’ in the problem is not specified. It appears that they read the puzzle as if they found one 20-dollar bill, and them was referring to bills.
One student wrote a thoughtful reply: Having more friends most likely wouldn’t change the amount of money found, considering the amount of money is independent of the number of people, meaning the friends would still find $20. However, with double the people, they may find more money in other locations. There is also a chance that the 2 extra friends would make the group walk a different path, meaning they wouldn’t find money at all.
Share:





17th September 2025, 01:21 pm
I recently posted the following puzzle about identical triplets.
Puzzle. Three brothers who are identical triplets live on the seventh, eighth, and ninth floors of the same apartment building. Their apartments are identical and vertically stacked. One day, all three step onto their balconies, standing in the same upright posture. The brother on the eighth floor shouts, “AAAA!” Which of the other two will hear him first?
Most readers got it right: our mouths sit lower than our ears. That means the distance from the mouth of the brother on the eighth floor to the ears of the brother on the seventh floor is shorter than the distance to the ears of the brother on the ninth floor. So the seventh-floor brother hears it first.
However, one reader, Ivan, taught me something I didn’t know: identical twins aren’t always identical. He even sent a photo of Mark and Scott Kelly — identical twins of different heights.
Of course, as a first approximation, we can assume identical triplets are identical. But mathematicians are nitpicky and like precision. Ivan (clearly a mathematician at heart) also noted that even identical twins might wear shoes with different heel heights, which could tweak the distances.
Here’s another reader submission that made me smile:
- The seventh-floor brother will hear it first, because the eighth-floor brother has fallen off the balcony and is screaming as he plummets towards the earth.
Nitpicking again: that’s a stretch, since the problem says they’re standing — but it’s still funny.
Share:





13th September 2025, 12:47 pm
Here’s a problem from our 2025 STEP entrance test, taken by nearly a hundred students.
Problem. Pavel likes pets. All his pets except two are dogs. All his pets except two are cats. All his pets except two are parrots. The rest of the pets are cockroaches. How many pets of each kind does Pavel have?
Here is a solution from one student: one cat, one dog, and one parrot. No cockroaches—phew. Most students (and ChatGPT) found this one. By the way, I ran my whole test through ChatGPT, and this was the only mistake it made. ChatGPT, along with many students, missed the second solution: Pavel has two cockroaches.
Two more students’ answers made me smile:
- His pet cockroach is named Two. It follows that Pavel has zero cats, zero dogs, zero parrots, and one cockroach named Two.
- The parrots would eat the cockroaches, the cats would eat the parrots, and the dogs would eat the cats. Whatever he has now, he’ll be left with only dogs.
Share:





27th August 2025, 10:49 am
Here’s a neat coin puzzle I received by email from my reader s_hskz2 (at twitter.com).
Puzzle. You have 9 coins: 3 gold coins, 3 silver coins, and 3 bronze coins. Within each metal, the coins are indistinguishable. Exactly one gold, one silver, and one bronze coin are counterfeit; the other six are genuine. You are provided with a magic bag that functions as follows: when you place a subset of coins into the bag and cast a spell, the bag glows if and only if the subset contains all three counterfeit coins. Can you identify all three counterfeit coins using at most 5 tests?
I tried to find an easy solution and didn’t. Then I decided to use information theory to guide me to an answer. Unsurprisingly, it worked. The solution wasn’t trivial, but it was a lovely practice in using information theory for such puzzles.
Later, s_hskz2 sent me a more difficult version: There are 10 coins of each kind, and you are allowed to test 10 times, but I was too lazy to try.
Share:





26th August 2025, 11:44 am
Puzzle. Three brothers who are identical triplets live on the seventh, eighth, and ninth floors of the same apartment building. Their apartments are identical and vertically stacked. One day all three step onto their balconies, standing in the same upright posture. The brother on the eighth floor shouts “AAAA!” Which of the other two will hear him first?
I gave this puzzle to my students, and two of them offered the right answer for the wrong reasons. One said, “The seventh-floor brother, because air is warmer closer to the ground and sound travels faster in warmer air.” Another said, “The seventh-floor brother, because the air is denser at lower altitude and sound travels faster in denser air.”
What is the right reason?
Share:





28th December 2024, 12:09 pm
Once, I gave a puzzle to my students as homework just to check their level of attention.
Puzzle. A family has two identical twins. One of them is a boy, what is the probability that the other one is a boy?
What can I say? Some of the students didn’t pay attention and gave weird answers like 1/2, 1/3, and 2/3.
The twins are IDENTICAL. The other one has to be a boy! Duh!
One of the students was well-educated and mentioned that it is theoretically possible for different twins to be different genders, though this is extremely rare. When one fertilized egg splits into two, producing two embryos, the genetic material of both eggs is the same, almost. Some errors during splitting are possible, and it seems that some very particular errors can lead to the identical twins being identified as a boy and a girl. I never knew that before!
However, one student thought outside the box. In his vision, a family adopted two identical twins who aren’t each other’s twins, just happen to be identical twins with someone else.
Share:





24th December 2024, 04:55 pm
18th November 2024, 12:57 pm
A new hat puzzle from Gribalko, reminding me of traffic lights.
Puzzle. You and six of your mathematician friends each have a hat placed on your head. Each of you can see the hats of all the others but cannot see your own. You were all told that there were three red, three yellow, and three green hats in total, but two of them were hidden. Your friends began to say the following phrases in sequence:
- First: “I don’t know what color my hat is.”
- Second: “I also don’t know what color my hat is.”
- Third: “I also don’t know what color my hat is.”
- Fourth: “I know that my hat is red.”
- Fifth: “But I still don’t know what color my hat is.”
- Sixth: “And I am sure that my hat is yellow.”
Can you determine what color hat you have on your head?
Share:





13th November 2024, 03:30 pm
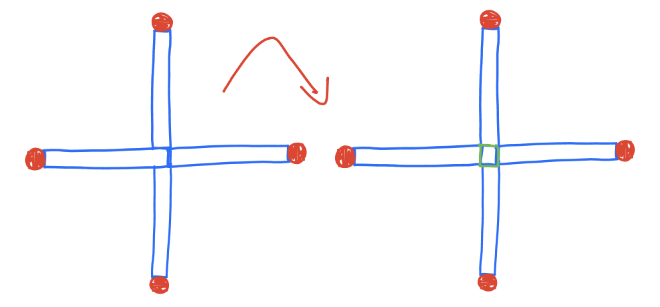
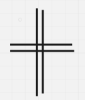
I once saw a TikTok video featuring a puzzle: four matches were arranged to form a plus sign, and the challenge was to move one match to create a square. The solution shown differed from what first came to my mind, so I decided to share the puzzle with my students. Instead of drawing a diagram, I described it to them in words.
Puzzle. Arrange four matches to form a plus sign. Move one match to form a square.
Most of my students gave the same solution shown in the video: moving one match slightly away from the center to create a square in the center, with the inner edges of the matches forming its borders. Not all the students were as lazy as I was; some drew pictures to illustrate. One example is shown below, where the resulting square is in green.
My solution, also discovered by a couple of students, was to move one match to form the number 4, which is a square.
I am glad I didn’t provide a picture because it led to two unexpected solutions. For the first one, imagine a 3D shape out of four matches where one projection forms three sides of a square, and the other one is a plus sign. We can take the match from the plus sign that is not a side of a square and use it to complete the square. The second solution is shown below. The arrangement already contains a small square, so you can take a match and put it back. Being lazy brings benefits!
Share:





5th November 2024, 12:36 pm
Here is another riddle I discovered in a book and gave as homework to my students.
Puzzle. I can use the number 20 thrice to make 60: 20 + 20 + 20 = 60. Make it 60 again by using a different number three times.
The book’s answer was to use 5: 55 + 5 = 60.
My students were very inventive. All of them solved the puzzle, but only one out of ten students came up with the book’s answer.
- For most of them, the new number was 60, as in 60 + 60−60 = 60, or 60*60/60.
- Some used −60 or 1/60, as in −60 − (−60) − (−60) = 60, or ((1/60)/(1/60))/(1/60) = 60. Similarly, some multiplied the cube root of 60 three times.
- One student used 59 in a clever way, as in 59 + 59/59 = 60.
- Another student said the following. If you turn 60 upside-down, you will make 09, and now you can use the number 3 thrice: 3+3+3 = 09.
- And the last on my list is the student who said that 42 has to be the answer to the universe and everything. He summed up two instances of 42 to get 84 and then subtracted the third instance of 42 with the digits flipped to get 84 − 24 = 60.
Share: