This essay is written especially for high school and undergrad math lovers who enjoy problem solving and who plan to major in mathematics. One of the authors, Tanya, often received this advice when she was an undergraduate in Russia: “Problem solving is child’s play. You’ll have to change your attitude if you plan to succeed in research.”
Perhaps that’s why some famous problem solvers, even those who won gold medals at IMO, became not-so-famous mathematicians. To help you avoid that fate, we’ll discuss the ways in which research is unlike problem solving.
Is research different from problem solving?
Yes and no. There are many mathematicians who continue problem solving as their form of research. Remember Paul Erdos who used to suggest a lot of problems and even offered money rewards for solutions. Many mathematicians solve problems posed by other people. You might consider Andrew Wiles as the ultimate math problem solver: he proved Fermat’s last theorem, which had been open for 400 years. Though he could not have done it without the many theories that had already been generated in the search to find the elusive proof.
You can become a mathematician and continue to look around you for problems to solve. Even though this is still problem solving, the problems will be very different from competition problems, and you will still need to adjust to this type of research.
Problems you solve during research
So, what is the difference between problems that mathematicians solve during competition and the problems they tackle for their research?
Expected answer. In competition problem solving you know there is a solution. Often you know the answer, but you just need to prove it. In research there is no guarantee. You do not know which way it will go. For this reason finding counter-examples and proving that some ideas are wrong is a positive contribution, for it can eliminate some possibilities. So one adjustment is that you might start valuing negative answers.
Difficulty level. Competition problems are designed to be solved in one hour, so you are expected to generate an idea in just minutes. In research the problem might drag on for years, because it is far more difficult. If you get used to the instant gratification of competition problem solving, you might find the lengthy work of research frustrating. It’s very important to adjust your expectations so that you won’t drop a problem prematurely. You need to measure progress in small intermediate steps and learn to appreciate this different rhythm.
Motivation. Although you miss the euphoria of finding quick solutions, you get a different kind of reward with research. Because no one knows the answer in advance, when you solve the problem, you are the first to do so. You have opened up a new truth.
Time limits. In competitions you have a time limit for every problem. In research you set your time limits yourself. That allows you to put a problem aside and come back later if necessary. In a sense you can think about several problems at the same time.
Your passion. You can choose your problems yourself. Research is much more rewarding if you follow your heart. In competitions you have to spend time on problems you might not like. Here you have an option to choose and pick only the problems that appeal to you. Thus, you become more motivated and as a result more successful.
Finding a problem
After solving problems posed by other people, the next step is to pose math problems yourself. As we mentioned before, in research you do not always have a strictly-defined problem. It is a significant adjustment to move from solving already-defined problems to posing the problems yourself.
Generalizations. Often you can generalize from an existing problem to more general cases. For example, if you see a problem for n=3, you can wonder what happens for any n, or for any prime n.
Being on the lookout. Sometimes a situation puzzles you, but you can’t formulate a specific problem around that situation. For example, why do most of the terms in the sequence end in 9? Is there a reason for that? Or, you might find that a formula from your integrable systems seminar is similar to a formula from your representation theory class. This might lead you to the essential research question: “What is going on?” You always need to be on the lookout for the right questions.
Value. When you create your own research problems it is crucial to always ask yourself: Is the problem I am creating important? What is the value of this problem? There is no a good reason to create random generalizations of random problems. If the problem you found interests you very much, that is the first sign that it might interest other people; nonetheless, you should still ask yourself how this problem will help advance mathematics.
Mathematics is not only problem solving
There are other things to do than solve problems. There are many mathematicians who work differently, who don’t solve problems or don’t only solve problems. Here are some of the many options mathematicians have:
Building structures. You may not be interested in calculating the answer to a question, but rather in building a new structure or a new theory.
Advancing the language. When you invent new definitions and new notations, you will help to simplify a math language so that the new language will allow you to prove your results and other peoples’ results faster and clearer.
Unification. Sometimes you notice two results in two different areas of mathematics with some kind of similarity. Explaining why these results are the same might create a new understanding of things. It is great to unify two different areas of mathematics.
Explaining. Very often proofs are not enough. Why is something true? What’s the reason and what’s the explanation? It is good to ask yourself a “why” question from time to time, such as, “Why is this proof working?” When you find an answer, it might become easier to understand what to do next and how to generalize your proof.
Directions. Many mathematicians are valued not for the problems they solve or suggest, but for ideas and directions they propose. Finding a new direction for research can generate unexpected opportunities and create tons of math problems on the way. It can be valuable to come up with good conjectures, even if you have no hope of solving them yourself. Two example of this are the Weil conjectures (eventually proved by Deligne) and the Langlands program, which is still incomplete but which has generated a huge amount of important research.
Vision. What is the most general thing that can be proved by this technique? What kinds of improvements and refinements are there? It is good to step back from the problem you solved and meta-think about it.
As you can see, problem solving is just the beginning of all that mathematics can offer you. Mathematicians find these other options very rewarding, so it’s worth your while to try these varied aspects of mathematical work to see if you have a taste for other things. If you don’t venture beyond problem solving you might miss the full beauty of mathematics.
Share:





 Many people ask me when is a good time to teach kids math. In my experience, it can never be too early. You just need to keep some order. Multiplication should be taught after addition, and negative numbers after subtraction. Kids should remember multiplication by heart at the age of seven. They can understand negative numbers as early as four.
Many people ask me when is a good time to teach kids math. In my experience, it can never be too early. You just need to keep some order. Multiplication should be taught after addition, and negative numbers after subtraction. Kids should remember multiplication by heart at the age of seven. They can understand negative numbers as early as four.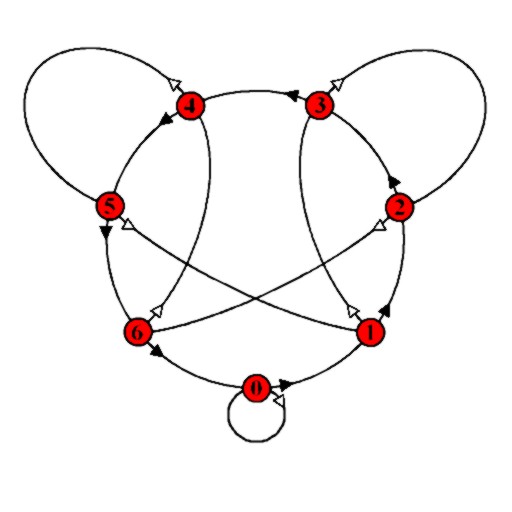 The graph is used in the same way as the first graph. To find the remainder on dividing a number by 7, start at node 0, for each digit D of the number, move along D black arrows (for digit 0 do not move at all), and as you pass from one digit to the next, move along a single white arrow.
The graph is used in the same way as the first graph. To find the remainder on dividing a number by 7, start at node 0, for each digit D of the number, move along D black arrows (for digit 0 do not move at all), and as you pass from one digit to the next, move along a single white arrow. Here is a fun math activity I use with my students, after I teach them to play
Here is a fun math activity I use with my students, after I teach them to play  While they’re building them, I ask a lot of questions, from how many cards there should be in the deck to how many different sets there are.
While they’re building them, I ask a lot of questions, from how many cards there should be in the deck to how many different sets there are.
