Tanya Khovanova's Math Blog

I got immediately attracted to the puzzle Oleg Polubasov recently posted on Facebook.

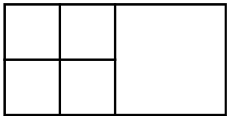
Puzzle. A rectangular clearing in a forest is an N-by-M grid, and some of the cells contain a tower. There are no towers in the cells that neighbor the forest. A tower protects its own cell completely and parts of the eight neighboring cells at a depth of half of a cell. Here by neighbors, we mean the cells horizontally, vertically, and diagonally adjacent to the given cell. In particular, if each cell is one square unit, a tower protects four square units. The protected area forms a square with borders that lie in between the grid lines. A tsar knows the towers’ locations and wants to calculate the protected area. Prove that the following formula gives the answer: the number of 2-by-2 subgrids that contain at least 1 tower.

I like this puzzle because it has an elegant solution. But there is more. The puzzle reminds me of one of my favorite novels by Arkady and Boris Strugatsky: The Inhabited Island, also known as Prisoners of Power. This is a science fiction novel where Max Kammerer, a space explorer, ends up on a planet with desolate people who, twice daily, experience sudden bouts of enthusiasm and allegiance to the government. Later, it becomes clear that the love for the rulers comes from towers that broadcast mind-control signals suppressing critical thinking and making people prone to believe propaganda.

The novel was written in 1969 but accurately describes the modern Russian propaganda machine. It appears that there is no need for a secret signal. Just synchronized propaganda on government-controlled TV turns off people’s brains.

A Whitney umbrella is a cool surface I wanted to crochet. The umbrella continues to infinity, and there is no way I want to crochet the whole thing. I wanted to make a finite portion of a Whitney umbrella surrounding the most exciting point.

The result is seen in the picture. Technically, I crocheted not Whitney umbrellas but topologically equivalent surfaces. I am most proud of my secret — and painful — method of crocheting the self-intersecting segment. One day I will spill it.

As Wikipedia defines it: the Whitney umbrella is the union of all straight lines that pass through points of a fixed parabola and are perpendicular to a fixed straight line parallel to the parabola’s axis and lies on its perpendicular bisecting plane. If you look at the picture, the fixed straight line is the self-intersection line, which is a continuation of the line segment where the colors are woven through each other. You can find the parabola as the curve formed by the two-colored edge on either side of the umbrella. Oops, I forgot that only three of these umbrellas are made of two colors.

The Whitney umbrella is a ruled surface, meaning that for every point, there is a straight line on the surface that passes through the point. A ruled surface can be visually described as the set of points swept by a moving straight line.

Oh, look, the stitched rows can pretend to be these straight lines. Actually, if I fold these thingies, the stitched rows ARE straight lines. But, when I make the edges into parabolas, the rows stop being straight. In the real Whitney umbrella, if you look along the intersection line, the straight lines are closer to each other than they are along the parabola. But in crochets, the distances between rows have to be fixed. If my crochets are folded, they become rectangles and ruled surfaces. The real Whitney umbrella does not fold into a plane.

The Whitney umbrella is famous for being the only stable singularity of mappings from R² to R³. I am grateful to Paul Seidel for emailing me the proof. This singularity is so famous it even has two names: pinch point and cuspidal point. Though my crochets are not exactly Whitney umbrellas, they show this singularity. Hooray! I found a secret way to crochet the most famous stable singularity!

My favorite of the Escher plane tessellations is the one with shells. It is stunning, and the mathematics behind it is beautiful. I want to thank the late John Conway for teaching me the secret of this drawing.

Mathematicians are interested in tessellations because of the symmetries behind them. This tessellation has translational and rotational symmetries. Can you find them?

When I ask my students to find the rotational symmetries, they immediately tell me that they see two different 4-fold points, aka points where 90-degree rotations preserve the drawing. One point, I call G, is where four greenish shells meet, and one point, I call R, is where four reddish shells meet.

As you might have guessed, the students’ answer is not quite correct. There is more to the picture. Look at a dark-brown shell that looks like a curvy rectangle. This shape has markings. Now look at a specific point R and its four closest brown shells. You can see that going around this point R, the brown shells alternate their orientation: the darker side of these shells either faces towards point R or away.

The big secret of this artwork is that it contains TWO symmetry groups: a group and a subgroup. If we ignore the markings on the brown shells and consider them one solid color, then point R is indeed a 4-fold symmetry point. In addition, the center of the brown shape is a 2-fold symmetry point. Thus, the symmetry group of this simplified drawing is 442 in orbifold notation.

If we take the markings of the brown shells into account, then point R is not a 4-fold rotation, it is a 2-fold rotation. Point G keeps the property of being a 4-fold rotation. If you know your symmetry groups, you can conclude that there should be another 4-fold rotation. But where is it?

I will spill my answer. The symmetry point G is not ONE symmetry point anymore. There are two different points where greenish shells meet. The dark side of the brown shells faces one of them and looks away from the other.

The dark secret of this drawing is that it demonstrates two symmetry groups: group 442 and its subgroup 442, with different fundamental regions. To see the secret, you must look closely at a dark brown shell and find its darker side.

Here is one of my all-time favorite problems.

Puzzle. Four glasses are placed on the four corners of a square rotating table; each glass is either right-side up or upside down. You need to turn them all in the same direction, either all facing up or all down. You may do so by grasping any two glasses and turning either none, one of them, or both over.
There are two catches: 1) You are blindfolded, and 2) the table is spun after each round. Assuming a bell rings when you have them all facing the same way, how do you do it?

When I first heard this problem, the person who tortured me with it forgot to mention the bell. The problem was impossible: there was no feedback. Then, the bell was mentioned. It was an aha moment: you get information, but only a confirmation that the problem is solved. I tried to think about the puzzle backwards. What could be my last step? Assume that I know that the glasses alternate around the table: up, down, up, down. Then, as my last step, I can reach for the diagonal glasses and turn them over.

This is how you might start thinking about this puzzle. You can find the rest of the solution on the puzzle’s Wikipedia page.

Here is a wonderful variation, proposed by Michael Hotiner from Ukraine, that appeared ten years ago at a puzzle competition. This variation is not cheap; the players must pay with their lives, albeit virtual ones.

Puzzle setup. Consider a computer game where at level M, there is an M-sided rotating table with glasses at each corner. The setup is similar to the four-glasses puzzle above. The player is blindfolded, and the table rotates between rounds. As soon as level M is over, if all the glasses face one direction, the bell rings, and the player moves to the next level, M+1.
At each round, the player can decide on the number N of glasses to touch. Upon deciding, they have to pay N! lives for that round. Then, the player can touch the glasses one by one, choosing the next glass depending on how the previous glasses are oriented. After all the glasses are touched, the player can decide which ones to turn upside down.

Let’s see what happens at the very beginning of this game. The game starts at level 1, with only one glass. The round is solved before it starts. The cost is 0. The bell rings, and the game immediately goes to level 2.

Consider level 2. If the bell doesn’t ring immediately, the glasses face different directions. The cheapest way to proceed is to choose N = 1 and turn any glass. The cost is 1.

Consider level 3. A player can solve it in one round by touching all three glasses and turning them the same way. The cost is 3! = 6. There is a cheaper method that costs 4 lives in two rounds. In the first round, the player can touch any two glasses and turn both of them up. If the bell doesn’t ring, then the third glass is upside down. In the next round, the player can touch two glasses. If one is upside down, that glass should be turned up. If both glasses are right side up, then the player should turn both of them over to finish the round.

Puzzle tasks.

1. Find a way to pass level 3 using only three lives.
2. Find the cheapest way to pass level 4.
3. Find the cheapest way for level 6.
4. Find a way to pass level 5 using only 30 lives.

“Do you really hope to get hired here? We will never hire a woman physicist.” This was my friend’s job interview here in the US, though many years ago.

Another friend had an adviser who insisted that to recommend her for a PhD he needed to get into her pant first.

I heard more stories over the years, but my personal experience with gender bias was not so dramatic. Or, it could be that I didn’t pay attention. Let me start with my most memorable story.

Why did I get an NSF postdoc? Thirty years ago, I had recently arrived in the US, and just had a baby. A friend suggested that I apply for an NSF postdoc. I applied, and I got it. I was elated, but my happiness didn’t last long. It lasted until some bitter guy, who didn’t get into a postdoc, told me I got the position only because I was a woman. This was the first time I heard that gender might play a role in such decisions. I was devastated. To this day, I still do not know whether it was my talents or my gender that got me the postdoc. For many years after, I had impostor syndrome.

I wrote a blog essay, Polite Gender Bias, about some of my other stories. Each individual case might not seem gender-related, but they were repeated too many times, so I became sensitive. I call these stories:

• An unbelievably amazing proof.
• Simple versus elegant.
• Saying “I am dumb” as a defense.
• Who generates ideas for Tanya Khovanova’s math blog?

Here is a more recent story. I do not know whether I should be proud, angry, or embarrassed.

Where is the sugar? From time to time, in the MIT math department tea room, I am asked where is the sugar, or some similar things. This often happens when there are several males in the room. Why was I chosen? It could be that I look friendly and have a great smile, and this is why people approach me. Or people might assume that, being a woman, I am a secretary who knows everything about the kitchen. Or, they might assume that, being overweight, I love sugar and know about every secret sugar stash in any kitchen.

Here is a story where I know exactly how I felt: I was angry.

Can I say a word? I was invited to a lunch discussion on gender issues at our MIT math department. I am not faculty, so I was sure the only reason I was there was because they wanted more female participants. People around me enthusiastically praised our department’s handling of gender issues. I tried to speak many times, but some guy would always interrupt me. I was about to start laughing very loudly at the irony of the situation when our department head finally noticed what was going on and gave me a chance to say a word. The situation was resolved then, but I regret that I didn’t start laughing.

As stories pile up, I become more vocal. I am tired of being nice at my own expense. Now people think I am a bitch. So be it.

Putin’s bodyguards `collect his excrement on trips abroad and take it back to Russia with them’. This was an article in the Independent. Presumably, Putin is afraid that someone can analyze his waste to get information about his health. Here is a quote from the article.

According to the report, members of the Russian president’s Federal Protection Service (FPS) are responsible for collecting his bodily waste in specialised packets which are then placed in a dedicated briefcase for the journey home.

Here is my joke on the subject.

Joke. Putin’s guard collecting his waste wrote a book of memoirs. The book has two chapters: Number One and Number Two.

One of my all-time favorite puzzles is about tiling a chessboard with 1-by-2 dominoes. But the chessboard is special: two cells at the opposite corners are removed. A similar elegant chessboard puzzle recently appeared on Facebook.

Puzzle. Our special chessboard has one corner cell removed. On each of the remaining cells, there is an ant. At a signal, each ant moves two cells horizontally or vertically (for example, an ant can move from b3 to b5). Is it possible that after all the ants perform their move, each of the 63 cells will have an ant?

This puzzle is a variation of another puzzle, where all the setup is the same, but each ant moves only one cell horizontally or vertically. You can start with this variation, as it is easier.

This puzzle was in a homework assignment I gave to my students.

Puzzle. In the given configuration of matches, move two matches to form three squares.

I assume that the intended solution is the one below. Its appeal is that it has three squares of the same size and no dangling matches.

As usual, my students were inventive and suggested many alternative solutions.

• The first picture shows a solution with three squares of different sizes: two small ones and one twice as big.
• The next solution has two big squares and one smaller one.
• The following picture shows three squares of different sizes.
• Since the problem doesn’t forbid forming more than three squares, there are, of course, many solutions with more than three squares. The last picture has six squares.

A Facebook Challenge

I recently stumbled upon the following challenge on Facebook.

Puzzle. Type the number of seconds in a week using the smallest number of characters.

I lied. The challenge was to type the same number using the smallest number of clicks on a computer keyboard. There is a slight difference, and I like my version better.