Tanya Khovanova's Math Blog

Alex Bellos sent me his new book Puzzle Ninja: Pit Your Wits Against The Japanese Puzzle Masters. What has he done to me? I opened the book and couldn’t close it until I solved all the puzzles.

This is a fantastic book. There are many varieties of puzzles, including some types that I’ve never seen before. Also, the beautifully designed puzzles are great. Often puzzles of the same type target different solving ideas or have varied cool themes.

This book is more than a bunch of puzzles; it also contains poetic stories about puzzle histories and Japanese puzzle designers. Fantastic puzzles together with a human touch: this might be my favorite puzzle book.

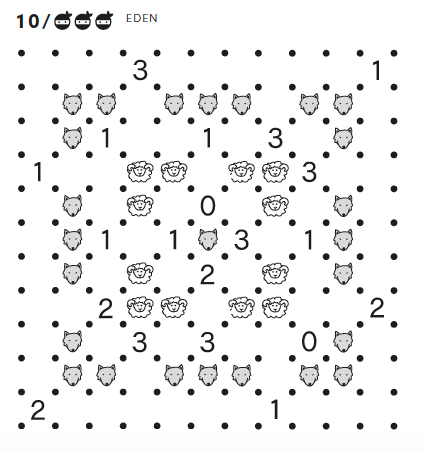
I present two puzzles from the book. The puzzle type is called Wolf and Sheep Slitherlink. The Slitherlink is a famous puzzle type with the goal of connecting some of the neighboring dots into a single non-self-intersecting loop. A number inside a small square cell indicates how many sides of the square are part of the loop. Wolf and Sheep Slitherlink is a variation of Slitherlink in which all sheep should be kept inside the fence (loop) and all the wolves outside.

Ignore the numbers in the title as they just indicate the order number of Wolf and Sheep Slitherlink puzzles in the book. The number of ninja heads shows the level of difficulty. (The hardest puzzles in the book have four heads.) The difficulty is followed by the name of the puzzle master who designed the puzzle.

The first puzzle above is slightly easier than the second. I like the themes of these two puzzles. In the first one, only one cell—lonely wolf—marks the relationship to the fence. In the second one, the wolf in the center—who needs to be outside the fence—is surrounded by a circle of sheep who are in turn surrounded by a circle of wolves.

My friend Alex Ryba uses interesting math questions in the CUNY Math Challenge. For the 2016 challenge they had the following problem.

Problem. Eve owns two six-sided dice. They are not necessarily fair dice and not necessarily weighted in the same manner. Eve promises to give Alice and Bob each a fabulous prize if they each roll the same sum with her dice. Eve wishes to design her two dice to minimize the likelihood that she has to buy two fabulous prizes. Can she weight them so that the probability for Alice and Bob to get prizes is less than 1/10?

The best outcome for Eve would be if she can weight the dice so that the sum is uniform. In this case the probability that Alice and Bob get the prizes is 1/11. Unfortunately for Eve, such a distribution of weight for the dice is impossible. There are many ways to prove it.

I found a beautiful argument by Hagen von Eitzen on the stack exchange: Let a_i (correspondingly b_i) be the probabilities that die A (correspondingly B) shows i + 1. It would be very useful later that that i ranges over {0,1,2,3,4,5} for both dice. Let f(z) = ∑ a_izⁱ and g(z) = ∑ b_izⁱ. Then the desired result is that f(z)g(z) = ∑_j=0¹⁰ z^j/11. The roots of the right side are the non-real roots of unity. Therefore both f and g have no real roots. So, they must both have even degree. This implies a₅=b₅=0 and the coefficient of z¹⁰ in their product is also 0, contradiction.

Alex himself has a straightforward argument. The probabilities of 2 and 12 have to be equal to 1/11, therefore, a₀b₀ = a₅b₅ = 1/11. Then the probability of a total 7 is at least a₀b₅ + a₀b₅. The geometric mean of a₀b₅ and a₀b₅ is 1/11 (from above), so their arithmetic mean is at least 1/11 and their sum is at least 2/11. Therefore, the uniform distribution for sums is impossible.

So 1/11 is impossible, but how close to it can you get?

I just got this picture from my friend Victor Gutenmacher, which I never saw before. My 1975 IMO team is posing at our training grounds before the Olympiad trip to Bulgaria.

Left to right: Boris Yusin, Yuri Ionin, Zoya Moiseyeva (front), Gregory Galperin (back), me, Ilya Yunus, Valentin Skvortsov, Aleksandr Kornyushkin, Sergei Finashin, Sergei Fomin (front), Alexander Reznikov (back), Yuri Shmelev (front), Yuri Neretin (back), Victor Gutenmacher.

Our coaches are in the shot as well. Surprisingly, or not surprisingly, all of them moved to the USA. Yuri Ionin, now retired, was a professor at Central Michigan University. Gregory Galperin is a professor at Eastern Illinois University. Sergei Fomin is a professor at the University of Michigan. Victor Gutenmacher worked for BBN Technologies and Siemens PLM Software, and is now retired.

There are two more adults in the picture: Valentin Anatolievich Skvortsov, our leader and Zoya Ivanovna Moiseyeva, our deputy leader. Skvortsov was working at the math department of Moscow State University at that time. The University was angry that he didn’t block some students with Jewish heritage from the team thus allowing them to be accepted to Moscow State University without exams. I wrote a story of how Zoya persuaded Alexander Reznikov not to go to Moscow University to help Valentin. It ruined Alexander’s live, and didn’t even help Valentin. 1975 was Valentin’s last trip as the leader.

An orchestra of 120 players takes 70 minutes to play Beethoven’s 9th Symphony. How long would it take for 60 players to play the symphony?Share: