Tanya Khovanova's Math Blog

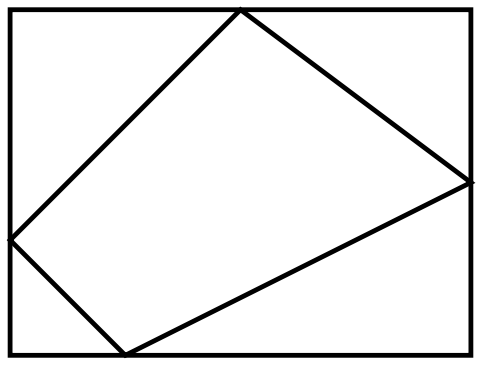
I recently posted A Quadrilateral in a Rectangle puzzle.

Puzzle. A convex quadrilateral is inscribed in a rectangle with exactly one quadrilateral’s vertex on each side of the rectangle. Prove that the area of the rectangle is twice the area of the quadrilateral if and only if a diagonal of the quadrilateral is parallel to two parallel sides of the rectangle.

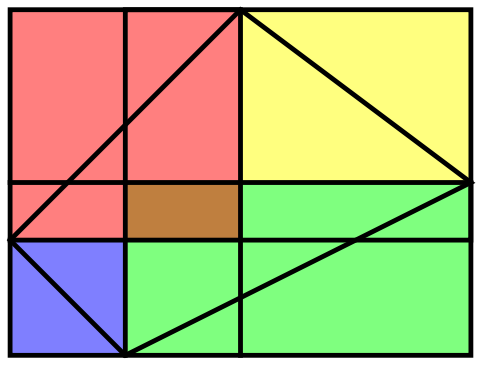
Now it is time for a solution where I use the sample rectangle pictured below. We draw lines parallel to the sides of the rectangle from every vertex of the quadrilateral. Now, we can find four pairs of congruent triangles where one triangle is inside the quadrilateral and the other is outside. In the picture below, the pairs are colored the same color. We see that green and red rectangles overlap, creating a brown rectangle. The fact that they overlap means that the quadrilateral’s area is less than half of the rectangle’s area.

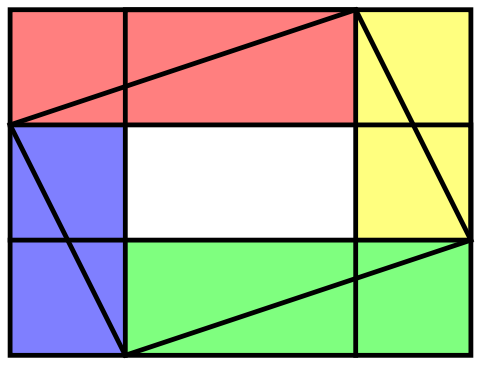
It could go the other way, as the next picture shows. Here, the quadrilateral’s area is more than half of the rectangle’s area. In this case, we have an “underlap” as opposed to an overlap.

Therefore, the quadrilateral’s area is exactly half of the rectangle’s if and only if there is no overlap/underlap, implying that the thickness of the overlap/underlap rectangle is zero. This means that one of the diagonals of the quadrilateral has to be parallel to two sides of the rectangle.

I recently posted the following polyomino puzzle, and my readers are asking for a solution.

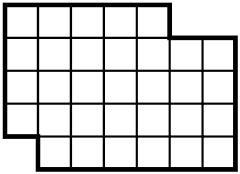
Puzzle. You are given a 5-by-7 rectangle with two corners cut out: A 1-by-1 tile is cut from the bottom left corner, and a 1-by-2 tile is cut out of the top right corner, as pictured. The task is to cut the resulting shape into two congruent polyominoes.

If a solution exists, there should be a transformation between the two congruent pieces. We can exclude a reflection and a central symmetry, as the union of the two shapes would have to be symmetric. We can exclude a translation: I leave it to the readers to explain why. What is left is a rotation or a glide. Let me remind you that a glide is composed of a reflection with respect to a line and a translation parallel to the line.

People often forget about glides, so this puzzle might be cool precisely because it is about glides. This is where we should start. We can safely assume that the top left corner belongs to piece A and, after the glide transformation, becomes the bottom right corner of piece B. It is also clear that the reflection line is parallel to the grid diagonals.

Then, we can start drawing the shapes. Piece A’s border starts from the top left corner and moves four squares down, then one square to the right, then one square down. Thus, piece B’s border starts at the bottom right corner and continues four squares to the left, then one square up, then one square to the left. In doing so, we reveal how the border of piece A continues. Thus, we can proceed in this manner to get the answer pictured below.

A new geometry problem from my friend, Alexander Karabegov.

Puzzle. A convex quadrilateral is inscribed in a rectangle with exactly one quadrilateral’s vertex on each side of the rectangle. Prove that the area of the rectangle is twice the area of the quadrilateral if and only if a diagonal of the quadrilateral is parallel to two parallel sides of the rectangle.

Here is another STEP homework question, which is a famous riddle.

Puzzle. Peter had ten cows. All but nine died. How many cows are left?

The wording is confusing on purpose. So, the students who are in a hurry subtract nine from ten and answer that only one cow is left. This answer is wrong. All but nine means that one cow died. So, the correct answer is nine.

One of my students decided that nine is the name of one of the cows, though it should have been capitalized. This means that all the cows except for Nine died, and only one cow, Nine, is left.

This student managed to find a legitimate explanation for the standard wrong answer.

Puzzle. A group of 20 students formed a line to take an oral exam with Professor Chill. They were afraid to enter the classroom, so they decided to do a drawing. They wrote the numbers from 1 to 20 on pieces of paper, placed them in a hat, and each student picked one. The student who drew the number 1 went into the classroom first. Then, the remaining 19 students repeated the process, writing down numbers from 1 to 19, and the one who drew the number 1 took the exam next. They continued this process until all 20 students had taken their exams. Remarkably, each student drew a different number each time. Olga drew number 14 in the first round. How many students took the exam before she entered the classroom?

Konstantin Knop posted the following puzzle on Facebook.

Puzzle. An agent sends messages to the command center. The messages have to be encrypted as a stream of 512 characters that can only be zeros and ones. Unfortunately, his transmitter is malfunctioning and gobbles 16 characters of each message. The missing 16 characters are always in the same positions in any message. As a result, the command center receives a sequence of 496 bits. Neither the center nor the agent knows which 16 bits of the sequence are eaten up by the device.
They cannot replace the broken transmitter. However, they can agree ahead of time to send K test messages, the content of which they both know. Find the smallest possible K needed to determine the positions of the disappearing 16 bits.

A quine is a computer program which takes no input and produces a copy of its own source code as its only output.

Puzzle. Assuming English is a computer language, write a quine in English.

My students had many solutions on how to solve this puzzle. They were all variations on “Write this sentence.” This is a self-referential sentence which doesn’t quite work. I even tried it on ChatGPT with the following result, “Of course, I’d be happy to help! Please provide the sentence you’d like me to write, and I’ll assist you with it.”

However, the solution I originally had in mind worked. ChatGPT repeated my input. So, ChatGPT provides a simple way for you to check your answer to this puzzle.

My students had more ideas. One of them suggested screaming at a friend, forcing the friend person to scream back. In a similar vein, one might say hello to a person in order to hear hello back. I tried this with ChatGPT, but it didn’t work. The bot replied, “Hello! How can I assist you today?”

Another trivial idea is to write nothing. This certainly works perfectly with ChatGPT.

What’s a polyomino? A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. Here, we have a puzzle about a polyomino that is almost a rectangle.

Puzzle. You are given a 5-by-7 rectangle with two corners cut out: A 1-by-1 tile is cut from the bottom left corner, and a 1-by-2 tile is cut out of the top right corner, as in the picture. The task is to cut the resulting shape into two congruent polyominoes.

Here’s another brainteaser from my friend, Alexander Karabegov.

Puzzle. Place the numbers from 1 to 8 at the vertices of a cube so that each face is balanced. On a balanced face, the sum of the numbers at the ends of one diagonal equals the sum of the numbers at the ends of the other diagonal.

My friend, Alexander Karabegov, sent me one of his puzzles. I love the mixture of algebra and calculus.

Puzzle. Describe a real quadratic function f such that the graph of its derivative f′ is tangent to the graph of f.