Divisibility by 7 is a Walk on a Graph, by David Wilson
My guest blogger is David Wilson, a fellow fan of sequences. It is a nice exercise to understand how this graph works. When you do, you will discover that you can use this graph to calculate the remainders of numbers modulo 7. Back to David Wilson:
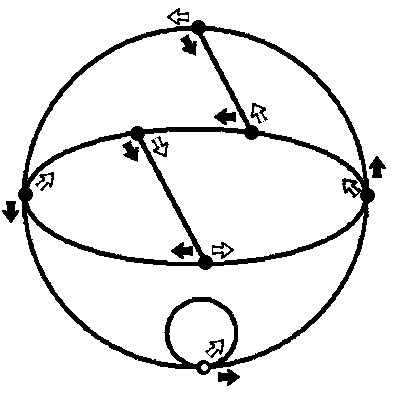I have attached a picture of a graph.
Write down a number n. Start at the small white node at the bottom of the graph. For each digit d in n, follow d black arrows in a succession, and as you move from one digit to the next, follow 1 white arrow.
For example, if n = 325, follow 3 black arrows, then 1 white arrow, then 2 black arrows, then 1 white arrow, and finally 5 black arrows.
If you end up back at the white node, n is divisible by 7.
Nothing earth-shattering, but I was pleased that the graph was planar.
Felipe Pait:
Are the divisibility graphs for other primes planar too? Are they easy to construct?
11 August 2009, 10:19 amLeo:
The graph of divisibility by 13 looks non-planar to me.
11 August 2009, 12:34 pmJeff:
Has anyone done a systematic study of diviability graphs in terms of other graph metrics? Is this already a defined corner of mathematics?
12 August 2009, 10:10 amAndrei Zelevinsky:
Nice idea! For my taste though I would sacrifice planarity and make the “remainders mod 7 clock” divided into 7 hours, with arrows 0 to 0, 1 to 3, 2 to 6, 3 to 2, 4 to 5, 5 to 1, and 6 to 4. Then say given n=325, you start at 0, take 3 steps clockwise, follow an arrow, take 2 steps clockwise, follow an arrow, take 5 steps clockwise and land at the remainder of 325 modulo 7.
12 August 2009, 11:31 amJames:
According to this, then, 5 is evenly divisible by 7. FAIL!
12 August 2009, 11:50 amJames:
Actually, I’m wrong — I didn’t count the dot at the end of the line segment joining the front and back of the horizontal circle.
12 August 2009, 11:53 amSeth Troisi:
5 is not evenly divisible by 7 on this graph.
Andrei Zelevinsky. I also like the mod 7 clock. I have used it in math projects once or twice.
12 August 2009, 2:03 pmShawn:
‘According to this, then, 5 is evenly divisible by 7. FAIL!’
I get stuck in the state right above the epsilon transition (the point with the left black arrow and right white arrow) from the start if I use 5. To me that doesn’t appear to say 5 is by 7…. Ouch…
12 August 2009, 3:28 pmMatt Might:
It is possible to construct a finite-state machine which determines divisibility for any divisor n.
There are n states: “0 mod n”, …, “n-1 mod n”. 0 mod n is the accepting state.
If you’re in state “k mod n”, and the next digit is d, then you got to state “k*b + d mod n” where b is the base of your number system.
12 August 2009, 4:09 pmDavid Wilson:
Let G(b,m) be the graph for base b >= 2 and modulus m >= 1.
The black edges (the clock edge) forms a Hamiltonian cycle H. Every other edge is incident on nodes in H (since H includes all nodes). If we number the nodes like a clock, 0 through m-1, then call edges (x1,y1) and (x2,y2) with x1 < x2 < y1 10,edges (3,6),(4,8),(5,10) are pairwise incompatible. Two of these three edges must be on the same side of H,and hence cross,destroying planarity of G(b,m). So b = 2 => m m = 4, (1,b),(2,2b),(3,3b) are incompatible, so b >= 4 implies m <= 3b. For any base b, there are a finite number of moduli m for which G(b,m) is planar.
I’m working on a program.
12 August 2009, 11:41 pmDavid Wilson:
A chunk of my post must have gotten deleted because it looked like an html tag. Sigh.
12 August 2009, 11:44 pmDavid Wilson:
For 2 <= b = 4, m = 2b+2 is the largest planar modulus. It appears that all the divisors of 2b+2, 2b and b-1 are planar. Moduli 1,2,3,4,5 and 7 are planar for every m.
b = 2: m = 1 2 3 4 5 6 7
b = 3: m = 1 2 3 4 5 6 7 8 9 10
b = 4: m = 1 2 3 4 5 7 8 9 10
b = 5: m = 1 2 3 4 5 6 7 8 10 12
b = 6: m = 1 2 3 4 5 6 7 9 12 14
b = 7: m = 1 2 3 4 5 6 7 8 9 10 11 14 16
b = 8: m = 1 2 3 4 5 6 7 8 9 11 16 18
b = 9: m = 1 2 3 4 5 6 7 8 9 10 14 18 20
b = 10: m = 1 2 3 4 5 7 9 10 11 20 22
b = 11: m = 1 2 3 4 5 6 7 8 10 11 12 14 22 24
b = 12: m = 1 2 3 4 5 6 7 8 9 11 12 13 24 26
b = 13: m = 1 2 3 4 5 6 7 8 9 10 12 13 14 26 28
b = 14: m = 1 2 3 4 5 6 7 10 13 14 15 28 30
b = 15: m = 1 2 3 4 5 6 7 8 9 10 14 15 16 30 32
b = 16: m = 1 2 3 4 5 7 8 9 15 16 17 32 34
b = 17: m = 1 2 3 4 5 6 7 8 9 10 12 16 17 18 34 36
b = 18: m = 1 2 3 4 5 6 7 9 11 12 17 18 19 36 38
b = 19: m = 1 2 3 4 5 6 7 8 9 10 11 18 19 20 38 40
b = 20: m = 1 2 3 4 5 6 7 8 10 14 19 20 21 40 42
b = 21: m = 1 2 3 4 5 6 7 8 9 10 11 14 20 21 22 42 44
b = 22: m = 1 2 3 4 5 7 9 11 21 22 23 44 46
b = 23: m = 1 2 3 4 5 6 7 8 10 11 12 14 16 22 23 24 46 48
b = 24: m = 1 2 3 4 5 6 7 8 9 10 12 16 23 24 25 48 50
b = 25: m = 1 2 3 4 5 6 7 8 9 10 12 13 14 24 25 26 50 52
12 August 2009, 11:54 pmInteresting Information: Divisibility by 7 using a graph « Use Your Illusion:
[…] leave a response I found this off this Math blog: https://blog.tanyakhovanova.com/?p=159 […]
15 August 2009, 11:05 amDavid Wilson:
Empirically, it looks like the graph for base b and mod m is planar if one of the following is true:
b == -1, 0, or 1 (mod m)
m is even and b == m/2-1 or m/2 (mod m)
m = 5 and b == 2, 3 (mod m)
m = 7 and b == 2, 3, 4, 5 (mod m)
m = 8 and b == 5 (mod m)
m = 9 and b == 3, 4, 6, 7 (mod m)
m = 10 and b == 3, 7 (mod m)
m = 11 and b == 7, 8 (mod m)
m = 14 and b == 9, 11 (mod m)
Proving it would be tough.
19 August 2009, 7:28 amAnup Pandey:
Want comments on this that i have had with me for decades now, none of my mathematician friends that I told this about have been of any help so far – I would LOVE your feedback on this.
Divisibility Rule for 7
by Anup Pandey
Discovered – 1985
Take a number n
if n is divisible by 7 then truncate((n+10)/10) + 2*(10-mod(n/10)) is divisible by 7
example take n = 49 then
truncate(59/10) = 5
mod(n/10) = 9
so then, 10-9 = 1
then 2* 1 = 2
so we get 5 + 2 = 7 which is also divisble by 7
Another example –
n= 434
truncate (444/10) = 44
2* (10-mod(434/10)) = 2*6 = 12.
So 12 + 44 = 56, which is divisible by 7
24 August 2009, 12:30 pmEmre Yucel:
Let’s simplify this…
25 August 2009, 11:01 amif n is divisible by 7 then truncate((n+10)/10) + 2*(10-mod(n/10)) is divisible by 7
if n is divisible by 7 then mod(n/7) is 0
Wiskundemeisjes » Blog Archive » Deelbaarheid door 7:
[…] de rest van een getal is bij deling door 7. Maar het is leuker om dat zelf uit te zoeken. En kijk hier voor de interessante reacties op haar stukje. « […]
2 September 2009, 3:01 amVincent:
Dear Anup
I hope you still read this. Let’s write n = 10x + y, with y between 0 and 9.
then truncate(n + 10)/10 = x + 1
and 2*(10 – mod(n/10) = 20 – 2y
So what you want to show is that if n = 10x + y is divisible by 7, then so is x + 21 – 2y.
Let’s go. First we see that if n is divisible by 7 then so is 5n. 5n = 50x + 5y.
But since 49 is divisible by 7 this means that x + 5y is divisible by 7 as well. (*)
7y is certainly divisible by 7 so substracting 7y from some number which is divisible by 7 doesn’t change anything.
We conclude from (*) that x – 2y is divisible by 7. Now since 21 is 3*7 it follows that x + 21 – 2y is also divisible by 7 and this is what we wanted to show.
How did you find this rule?
2 September 2009, 4:06 amFunny Little Puzzle « NOAM GR!:
[…] One of my favorite math blogs is Tanya Khovanova’s. Every so often she’ll post a neat meathematical construction or puzzle. This one she posted last week I thought was pretty neat. I guess it counts as both a […]
14 October 2009, 10:10 pmK. C. Koh:
I have programmed the algorithm by C language. You can down load the C source from the below site.
https://blog.joins.com/media/folderlistslide.asp?uid=kckohkoh&folder=75&list_id=11200986
By this program, you can check a large number(up to 100 digits which can be extended by simply increasing the size of array variables in the source). I would like share my program if you keep to notify that its athority belongs to me.
29 November 2009, 11:26 amLloyd:
For a number not divisible by seven (e.g. like the one used as n=325) the graph can also be used to find the nearest number which is divisible by 7. Go back to the node where you started tracking the final digit and count the black arrows required to take the shortest path back to the starting node. In the example used this is two so 322 is the nearest number to 325 divisible by 7. 🙂
12 April 2010, 11:48 pmClaude Miller:
I don’t mean to diminish your incite in obscure mathematics and simplified mind experiments, but a common blacksmith is infinitely more valuable to society than all of you mental masturbation.
Doc Miller
4 July 2010, 10:36 pmProton Zero:
I’ve found how to make such a graph for any positive integer:
For a given divisor n, assemble n nodes on a graph numbered 0 through (n – 1), where a node x has a black arrow pointing to node ((x+1) mod n). Given a numerical base b, m = ((b – 1) mod n), and each node x on the graph then gains a white arrow pointing to node ((x + x * m) mod n). Both black and white arrows can point a node to itself. Node 0 is the starting node.
Following those instructions will yield a graph like the one shown in this blog post (possibly planar, for higher numbers I don’t think it is).
I feel accomplished for figuring this out on my own :D.
5 July 2010, 2:46 amBrad Jolly:
There is a much easier way to determine whether a number is divisible by 7: chop, double, subtract. Chop the ones digit from the number, double it, and subtract it from the number formed by the remaining digits. The original number is divisible by 7 iff the difference thus obtained is divisible by 7.
For example, start with 3794. Chop the 4, double it (8) and subtract it from 379. The result is 371. Chop the 1, double it (2) and subtract from 37. The result, 35, is obviously divisible by 7; therefore, so is 3794 (and 371, for that matter).
I do hope that Claude Miller (above) will continue to share his special brand of mathematical “incite” with us. The man clearly possesses a superior intellect.
6 July 2010, 10:18 pmHarry:
@Proton Zero
11 July 2010, 12:32 amI was able to determine that the graph for the mod of 8 and 12 are non planar. In both cases, the graph contained a sub-graph which was a subdivision of K3,3. I didn’t bother to go beyond 12, but if anyone wants to, feel free.
Steven Miller:
Following the black arrows, number them 1 to 6 with the white dot 0. Where you stop will be the Modulus.
16 July 2010, 4:57 amfree math worksheets:
Thanks for sharing great article.
18 July 2010, 8:23 pmTanya Khovanova’s Math Blog » Blog Archive » Divisibility by 7 is a Walk on a Graph. II:
[…] was somewhat taken aback by the popularity of my earlier essay “Divisibility by 7 is a Walk on a Graph.” Tanya tells me it got a good number of hits. The graph in that article is rather crude, and […]
1 August 2010, 10:30 pmSigue el camino…módulo 7 | Gaussianos:
[…] grafo es una mejora de otro grafo del propio David Wilson que sólo nos indicaba si el número escogido era o no divisible entre 7. […]
19 August 2010, 1:01 amJeff:
I like the idea… and now to make a graph to check divisibility by 2. 🙂
12 October 2010, 11:10 amgeorge:
Where you stop will be the Modulus
26 November 2010, 11:36 amstephen:
maybe im doing it wrong but this says 71 and 710 are divisible by 7?
12 December 2010, 9:50 pmDaniele:
@stephen: Why should 71 emerge as divisible by 7?. Follow seven black arrows, ending up on the white dot; then change digit, by following the white arrows, which takes you back to the white dot; and finally follow a single black arrow (for the digit 1), and you are on a black dot, as required.
19 December 2010, 4:49 amBen:
I may be doing something wrong but according to this, 720 is divisible by 7. Am I doing something wrong?
18 April 2011, 5:30 pmViktor Engelmann:
look here:
https://algorithman.de/Algorithmen/fosap/coset_dfa.zip
it’s a program that constructs divisibility graphs for ANY number – and it’s even independent of the numeral system (so you can have a graph for divisibility by n in b-adic numbers, not only in decimal numbers)…
21 April 2011, 3:58 pmNumber Gossip, Travels and Topology « Math Munch:
[…] found this cool test for divisibility by 7 on Tanya’s website. Read about how to use it here, but basically you follow that diagram a certain way, and if you land back at the white dot, then […]
27 November 2011, 11:02 pmDivisibility by 7 | Fun With Num3ers:
[…] 5 black arrows. If you end up back at the white node, n is divisible by 7. Source: https://blog.tanyakhovanova.com//?p=159 Why does it work? GA_googleAddAttr(“AdOpt”, “1”); […]
30 April 2012, 1:25 pmLinks interessantes e Aplicações de Grafos | dremendes:
[…] caso, a divisibilidade por 7, no link que segue aqui, você pode ler o artigo. Mas se você tem preguiça eu […]
1 May 2012, 5:29 amFiroze:
I am NOT AT ALL a mathematician… but this was just too cool!! Thank you so much for sharing. 🙂
14 May 2013, 6:50 amOn aime, on partage #7 | Blog Objet Direct:
[…] https://blog.tanyakhovanova.com/?p=159 […]
31 May 2013, 12:57 amHow does the divisibility graphs work? – Math Solution:
[…] came across this graphic method for checking divisibility by […]
2 March 2022, 8:18 pmSigue el camino...módulo 7 - Gaussianos:
[…] grafo es una mejora de otro grafo del propio David Wilson que sólo nos indicaba si el número escogido era o no divisible entre […]
23 August 2023, 12:46 pm