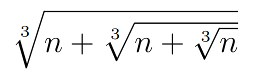Here is one of my all-time favorite problems.
Puzzle. Four glasses are placed on the four corners of a square rotating table; each glass is either right-side up or upside down. You need to turn them all in the same direction, either all facing up or all down. You may do so by grasping any two glasses and turning either none, one of them, or both over.
There are two catches: 1) You are blindfolded, and 2) the table is spun after each round. Assuming a bell rings when you have them all facing the same way, how do you do it?
When I first heard this problem, the person who tortured me with it forgot to mention the bell. The problem was impossible: there was no feedback. Then, the bell was mentioned. It was an aha moment: you get information, but only a confirmation that the problem is solved. I tried to think about the puzzle backwards. What could be my last step? Assume that I know that the glasses alternate around the table: up, down, up, down. Then, as my last step, I can reach for the diagonal glasses and turn them over.
This is how you might start thinking about this puzzle. You can find the rest of the solution on the puzzle’s Wikipedia page.
Here is a wonderful variation, proposed by Michael Hotiner from Ukraine, that appeared ten years ago at a puzzle competition. This variation is not cheap; the players must pay with their lives, albeit virtual ones.
Puzzle setup. Consider a computer game where at level M, there is an M-sided rotating table with glasses at each corner. The setup is similar to the four-glasses puzzle above. The player is blindfolded, and the table rotates between rounds. As soon as level M is over, if all the glasses face one direction, the bell rings, and the player moves to the next level, M+1.
At each round, the player can decide on the number N of glasses to touch. Upon deciding, they have to pay N! lives for that round. Then, the player can touch the glasses one by one, choosing the next glass depending on how the previous glasses are oriented. After all the glasses are touched, the player can decide which ones to turn upside down.
Let’s see what happens at the very beginning of this game. The game starts at level 1, with only one glass. The round is solved before it starts. The cost is 0. The bell rings, and the game immediately goes to level 2.
Consider level 2. If the bell doesn’t ring immediately, the glasses face different directions. The cheapest way to proceed is to choose N = 1 and turn any glass. The cost is 1.
Consider level 3. A player can solve it in one round by touching all three glasses and turning them the same way. The cost is 3! = 6. There is a cheaper method that costs 4 lives in two rounds. In the first round, the player can touch any two glasses and turn both of them up. If the bell doesn’t ring, then the third glass is upside down. In the next round, the player can touch two glasses. If one is upside down, that glass should be turned up. If both glasses are right side up, then the player should turn both of them over to finish the round.
Puzzle tasks.
- Find a way to pass level 3 using only three lives.
- Find the cheapest way to pass level 4.
- Find the cheapest way for level 6.
- Find a way to pass level 5 using only 30 lives.
Share: